Markov Decision Processes
Revised June 11, 2024
Sequential decision making is a process in which an agent, given some information, makes a series of decisions, each producing an observable consequence that informs the next decision. The agent's goal is to optimize a performance metric over a specified time horizon. In reinforcement learning (RL), this process is formalized as the optimal control of an incompletely-known Markov Decision Process (MDP). An MDP can be represented as a collection of objects:
\[ \begin{equation*} \mathcal{M} = \langle \mathcal{S},\mathcal{A},P,R,\gamma \rangle \end{equation*} \]
where \(\mathcal{S}\) is a set of states, \(\mathcal{A}\) is a set of actions, \(P\) is a transition probability function, \(R\) is a reward function, and \(\gamma\) is a discount factor.
At each time step in which decisions are made \(t\), the agent has some information \(s_t \in \mathcal{S}\), called the state, about the environment in which it operates. Based on the information in \(s_t\), the agent selects an action \(a_t \in \mathcal{A}\). The environment receives action \(a_t\) after which it transitions to a new state \(s_{t+1} \in \mathcal{S}\) and provides feedback to the agent in the form of a reward \(r_{t+1} \in \mathbb{R}\).
The probability that an agent transitions from a current state \(s\) to a new state \(s'\) after taking an action \(a\) is determined by the state transition probability function \(P(s, a, s’) = \mathbb{P}[s_{t+1} = s’ \mid s_t = s, a_t = a]\). The probabilistic nature of this function reflects the inherent stochasticity of most systems, where outcomes are influenced by random factors or variables. Importantly, this stochasticity adheres to the Markov property, which asserts that the probability of transitioning to a specific state depends only on the current state and action, and not on any past states/actions \(\mathbb{P}[s_{t+1} | s_t, a_t, s_{t-1}, a_{t-1}, \dots] = \mathbb{P}[s_{t+1} | s_t, a_t]\).
The agent's reward at each timestep is determined by the reward function \(R(s, a) = \mathbb{E}[r_{t+1} \mid s_t = s, a_t = a]\), which gives the expected immediate reward for taking action \(a\) in state \(s\).
Alternative reward model
In some problems, a reward may additionally be based on \(s'\). This is equivalent to the model described above. Let \(R(s,a,s’)\) be the expected reward when action \(a\) is taken in \(s\) and the agent transitions to \(s'\). Then, we can obtain the model \(R(s, a) = \mathbb{E}[r_{t+1} \mid s_t = s, a_t = a]\) by defining:
\[ \begin{equation*} R(s,a) = \mathbb{E}[r_{t+1} \mid s_t = s, a_t = a] = \mathbb{E}_{s’ \sim P(s,a)} \left[ R(s,a,s’) \right]. \end{equation*} \]
The decision-making process in an MDP continues iteratively until a terminal state is reached or a predefined maximum number of time steps has elapsed. These processes can either be episodic or continuing. Episodic tasks can last for an arbitrarily long duration but must eventually terminate, with timesteps \(t = 1, 2, \ldots, T-1\) (where \(T < \infty\)), while continuing tasks do not terminate with timesteps \(t = 1, 2, \ldots\) extending indefinitely.
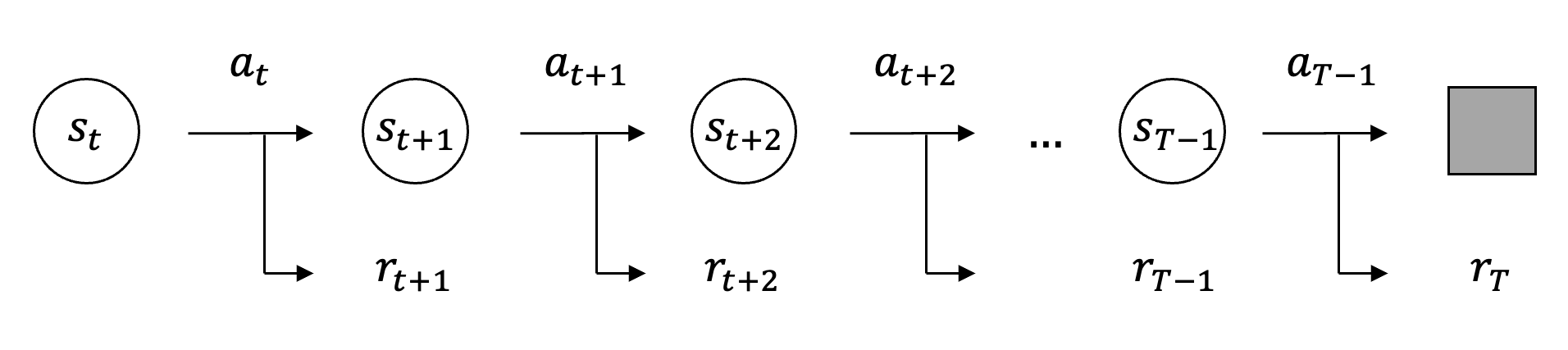 |
| A Markov decision process (MDP) is defined by the property that the current state \(s_t\) is sufficient (the Markov property), meaning the conditional distribution of the next state and reward depends only on \((s_t,a_t)\), i.e., \(\mathbb{P}(s_{t+1},r_{t+1}\mid s_t,a_t)\), with the policy specifying the distribution over actions. The agent's actions do not affect the fundamental rules or dynamics that dictate how states and rewards are generated by the environment but they do directly influence the specific outcomes and subsequent information the agent receives. Therefore, the agent cannot be myopic; it must account for and consider the long term consequences of its actions. |
In an MDP, an agent's performance is measured by its cumulative reward, or return. Cumulative reward can be computed in several ways, such as by summing or averaging the rewards received at each timestep. In practice, however, we commonly measure return by applying a discount factor to future rewards, which is an asymptotic weighted sum of rewards:
\[ \begin{equation}\label{eq:mdp-rewards} G_t = r_{t+1} + \gamma r_{t+2} + \gamma^2 r_{t+3} + \dots = \sum_{k=0}^{\infty} \gamma^k r_{t+k+1} \;, \end{equation} \]
where \(\gamma \in [0,1]\) is the discount factor. The discount factor quantifies the present value of future rewards — a reward received \(k+1\) time steps in the future is valued at \(\gamma^k\) times its immediate value. Discounting is both natural and intuitive. It aligns with human tendencies to prefer immediate gratification (similar to how immediate financial gains are favored due to the time value of money). Moreover, future rewards carry greater uncertainty compared to immediate rewards. Mathematically, using a discount factor \(<1\) prevents the possibility of infinite returns in cyclic or indefinitely long decision-making processes.
Note that Equation \(\eqref{eq:mdp-rewards}\) assumes the MDP is continuing. When measuring returns in episodic tasks, where the process concludes after a finite number of timesteps, the formula for returns requires a slight modification:
\[ \begin{equation}\label{eq:finite-mdp-rewards} G_t = \sum_{k=0}^\color{red}{T-t-1} \gamma^k r_{t+k+1} \;, \end{equation} \]
where \(T\) is the finite horizon, or the episode's endpoint.
Regardless of whether the task is episodic or continuing, the agent cannot be myopic. That is, it must consider both the short- and long-term consequences of its actions. By construction, both \(\eqref{eq:mdp-rewards}\) and \(\eqref{eq:finite-mdp-rewards}\) capture this tradeoff.
References
- Markov Decision Processes, Lectures on Reinforcement Learning (2015)
David Silver
- Markov Decision Processes: Discrete Stochastic Dynamic Programming (1994)
Martin L. Puterman
- Algorithms for Reinforcement Learning, Synthesis Lectures on Artificial Intelligence and Machine Learning (2019)
Csaba Szepesvari
- Reinforcement Learning: An Introduction (2018)
Richard S. Sutton and Andrew G. Barto
- MDPs, Reinforcement Learning (2019)
Shipra Agrawal